AGRIPPA

Henrique Cornélio Agrippa Von Nettesheim

(Colônia, Alemanha 1486 – Grenoble, França, 1535)

 

É considerado como o fundador da filosofia oculta 

e deixou a fama de “príncipe dos mágos”,  título que o acompanha até hoje.  Foi o grande rebelde da Renascença.

Nasceu em 1486, em Colônia, Alemanha e morreu em Grenoble no dia 18 de fevereiro de 1535. Filho de antiga família nobre estudou na Universidade de Colônia, foi médico, jurista, filósofo, cabalista e estudou também a alquimia. Aos vinte anos de idade já havia estudado a magia e a cabala; sabia oito línguas, dentre as quais, o hebreu.Sua vida acidentada foi uma sucessão de honras e de infortúnios, durante muito tempo atuou em missões diplomáticas e militares a serviço de diversos soberanos.
Como erudito, correspondeu-se com os grandes humanistas da época tais como: Melâncton, Erasmo, Cardeal Lourenço Campegi e Tritemo que foi seu amigo e mestre e que o influenciou a escrever sobre seus conhecimentos do oculto. Do Humanismo e do Aristotelismo da Idade Média, sucedeu-se o pitagorismo e o neoplatonismo, que na época começara a florescer, em seus estudos estavam: Plotino, Jâmblico, Porfírio e Pitágoras.Agrippa mergulhou no sobrenatural e no oculto a tal ponto, que o seu entusiasmo por tais filósofos, suplantou o seu sentido crítico de erudito.Por seu espírito aberto à todas as correntes do pensamento oculto, Agrippa tentou conciliar as diversas doutrinas ocultas e unir a filosofia à cabala. Em 1507, Agrippa desloca-se à Paris numa missão a serviço do imperador Maximiliano, aproveita para avistar-se com alguns jovens aristocratas com os quais forma uma sociedade secreta chamada Sodalitium (Comunidade), em conjunto elaboraram um plano místico para um mundo reformado e também um compromisso parta uma ajuda mútua.Em 1509, Agrippa chega a Dole, cidade em que Margarida da Aústria, filha de Maximiliano, era a soberana, através de um amigo, obteve autorização para lecionar literatura sagrada (Cabala) na Universidade.Iniciou pelo estudo do tratado cabalístico de Reuchlin: A Palavra Mirífica, também fez um estudo comparado das religiões. Embora afirmasse que a religião católica era a melhor, dizia que era necessário guardar em relação a ela, a liberdade de analise. Desejando agradar Margarida, escreveu: A Nobreza do sexo feminino e a superioridade das mulheres, com argumentos extraídos da Bíblia, de padres e da filosofia; ele elogia o sexo feminino em termos exaltados, dedica a obra à “divina Margarida, augusta e clemente princesa”. Por tudo isso, seus inimigos não tardaram a aparecer, especialmente do clero que viam na sua simpatia pela cabala judaica, uma perigosa heresia. Em Ghent, na Holanda, onde Margarida residia, o franciscano Catilenet, proferiu um sermão perante a princesa contra esse cabalista ímpio, Agrippa foi impedido pelos seus adversários de publicar a sua obra de elogio às mulheres e teve de abandonar a cidade. Em 1510 vai a Londres onde também formou um grupo da Sodalitium, em razão disso, tornou-se suspeito de ser um organizador da Fraternidade Rosa Cruz. Em Londres escreveu seus comentários às Epístolas de São Paulo. No ano seguinte foi para Colônia lecionar. Em 1515, Agrippa integra-se ao exército de Maximiliano que ia para a Itália, segue como cavaleiro dourado no campo de batalha. Pouco depois, o Cardeal de Santa Cruz envia-o a Pisa como representante junto ao Concílio, esta foi a sua última oportunidade de justificar a sua posição perante a Igreja e de agradar ao Papa Leão X, porém, o Concílio foi dissolvido e as assembléias interrompidas. Deixando sua carreira militar, Agrippa foi lecionar na Universidade de Pavia e depois na de Turim onde divulgou ensinamentos de Hermes Trismegisto, lá ficou até que a guerra o obrigou a partir, esteve durante sete anos na Itália. Graças ao apoio do marquês de Montferrat, Agrippa torna-se em 1518, síndico, advogado e orador da cidade de Metz, neste cargo ficou mais ou menos dois anos quando se demitiu após uma disputa com o inquisidor dominicano: Nicolas Savini. Mais uma vez atrai a cólera dos monges, por salvar da fogueira uma inocente camponesa de Woippy, injustamente acusada de bruxaria com base no testemunho de oito camponeses ébrios. Agrippa introduz uma petição junto ao bispo de Metz, faz libertar a mulher e pune com pesada multa os seus difamadores. Este acontecimento torna em breve, a situação de Agrippa insustentável e obriga-o a abandonar a região com sua mulher e filho. Volta a lecionar em Colônia e também em Genebra, em 1523 vai para Friburgo onde exerce a medicina, sua fama incita o bispo de Bazas: Synphorieu Bullioud a fazê-lo regressar à França e apresenta-o à corte. Em 1524 Agrippa é nomeado médico da duquesa Luíza de Sabóia, mãe do soberano Francisco I e passa a receber uma pensão. A duquesa pretendia que Agrippa também fosse seu astrólogo, o que ele recusa, pois acha que seus talentos mereciam ocupação mais importante. Quando a duquesa vai embora de Lyon, Agrippa ficou e seu nome foi excluído da lista de pensões. Sua sorte voltou em 1528 quando foi convocado por quatro protetores: Henrique VIII, da Inglaterra, o chanceler do imperador alemão, um marquês Italiano e Margarida de Austria, governadora dos Países Baixos, eles o nomearam historiador imperial. Nesta época escreveu: Da Incerteza e da Vaidade das Ciências e das Artes, onde afirma, antes de Rousseau, que as ciências e as Artes são prejudiciais ao homem, denuncia os abusos das profissões liberais do seu tempo em 103 capítulos, nas quais ataca ao mesmo tempo, os gramáticos, os músicos, os médicos e outros. Esta obra que teve duas edições em três meses, foi apreendida e queimada por ordem da Faculdade de Teologia de Paris, em janeiro de 1531.Agrippa estava em Anvers como conselheiro e historiador, a serviço do imperador Carlos V, seus amigos: o legado apostólico, cardeal Campegi e o bispo de Liege, cardeal de La Mark, tentaram defende-lo de seus inimigos, mas Agrippa perdeu seu cargo de historiador imperial e como ficasse impossibilitado de pagar suas dívidas, foi preso em Bruxelas, mas foi posto em liberdade um ano mais tarde. Dirigiu-se em 1532 para Bona onde tentou publicar a sua obra: Da Filosofia Oculta, verdadeira enciclopédia sobre magia, escrita em 1510 e que a havia submetido à crítica do seu mestre Tritemo, que após examiná-la, disse-lhe: “Tenho apenas mais uma advertência a fazer-vos, nunca esqueceis: ao vulgo falai somente coisas vulgares, reservai para vossos amigos todos os segredos de categoria superior, dai feno aos bois e açucar ao papagaio. Compreendei o que quero dizer, “para que não sejais espezinhado pelos bois”, o que freqüentemente acontece.Os trabalhos de impressão desta obra em três volumes foram interrompidos em 1533 por um pedido da inquisição ao Senado de Colônia, mas Agrippa protesta por carta aos magistrados e consegue publicá-la em julho do mesmo ano, em Antuérpia. Agrippa declarava que para ocupar-se da Magia, era necessário conhecer perfeitamente a física, a matemática e a teologia, para ele, a magia é uma faculdade poderosa, plena de mistério e que encerra um conhecimento profundo das coisas mais secretas da natureza, substâncias e efeitos, também suas relações e antagonismos. A física é terrestre, através dela conhecemos a natureza das coisas, a matemática é celeste, através dela aprendemos as dimensões e tamanho e podemos calcular o movimento dos corpos celestes; a teologia reporta-se ao mundo dos arquétipos, por ela atingimos o conhecimento de Deus, anjos, demônios, alma, inteligência e pensamento. No primeiro volume, sobre a Magia Natural, desenvolve a teoria dos três mundos: o elementar, o intelectual e o celeste; cada um sendo governado pelo seu superior e recebendo as suas influências. Analisa as virtudes ocultas das coisas, o modo como elas provêm das idéias, da alma, do cosmos e dos influxos planetários; quais as atrações e que repulsas suscitam nas espécies animais, vegetais e minerais. No 2º volume sobre os números, pesos e medidas, os segredos da harmonia universal, signos. No 3º volume ele trata o efeito dos nomes divinos, da hierarquia angélica, dos espíritos planetários, das nove classes de espíritos maus, dos ritos, conjurações, pantáculos sagrados, dos hieróglifos cabalísticos; tudo isso no intuito de instruir o mago; dizia: “Embora o homem não seja um ser imortal como o é o Universo, ele não deixa de ser dotado de razão e com sua inteligência, sua imaginação e a sua alma, é capaz de influenciar e transformar o mundo inteiro”. Agrippa defende a necessidade de religião em todo o cerimonial mágico, ele diz: “A religião é a coisa mais misteriosa e sobre ela devemos guardar segredo, pois é Trismegistro que afirma que constituiria ofensa à religião, divulgá-la à turba profana”. Na sua concepção, a religião é uma mescla de cristianismo, neoplatonismo e cabala. O seu tratado é uma síntese dos ensinamentos de Moisés, de Cristo, de Orfeu, de Demócrito de Pitágoras e de Plotino. Agrippa leu e tentou conciliar as escrituras com os textos sagrados das outras religiões, sobre as citações extraídas de autores estrangeiros, diz: “Eu não dou-as como verdade, é preciso ter a perspicácia para extrair o bem de todo o mal e reduzir a uma linha direita todas as coisas oblíquas. Concebeu a natureza como um conjunto vivificado em todas as suas partes por uma alma universal ou espírito do mundo que governa os elementos (Quinta essência) das leituras que lhes eram proibidas. Cimentou a idéia da magia primitiva sobre bases novas fazendo evoluir seu conceito em direção à ciência experimental com o estabelecimento da chamada magia natural, da qual foi o mais alto expoente juntamente com Paracelso. Alguns padres leram com entusiasmo “Da Filosofia Oculta”, outros evitaram-na com horror, porque viam nela a quinta essência das leituras que lhes eram proibidas. Em 1535 deixou Bona e regressa a Lyon, imediatamente Francisco I manda prendê-lo por ter usado afirmações satíricas: contra sua mãe, mas amigos seus conseguiram libertá-lo e ele buscou refúgio em Grenoble, na casade François de Vachon, que era presidente no Parlamento do Delfin. Agrippa Morreu no dia 18/02/1535, enterraram-no na Igreja dos Irmãos da Oração.. Foi sem dúvida, o ocultista mais importante da sua época, fundador da filosofia oculta, deixou a fama de “príncipe dos mágicos” que demorou muito tempo para desaparecer. Sobre uma de suas singularidades, conta Paul Jove: Agrippa estava sempre acompanhado por um grande cão negro, o qual chamava-se: Monsieur, era certamente o diabo…” esqueceu-se que Agrippa tinha também uma cadela com o nome de Mademoiselle. Assim as pequenas coisas de um autor anticonformista são viradas contra ele.

Proporções Humanas (Agrippa)

AS PROPRIEDADES GEOMÉTRICAS DE DUAS FIGURAS ILUSTRANDO AS PROPORÇÕES DO CORPO HUMANO POR HEINRICH CORNELIUS AGRIPPA

Tradução José Antonio de Souza Filardo  M.´. I .´.

 

Símbolos foram usados pelo homem primitivo como a forma mais antiga de escrita. Com muitas ilustrações simbólicas, grande cuidado foi tomado para enfeitar, decorar e adornar o símbolo; algumas vezes para esclarecer o significado simbólico e em outras para ocultar ou ofuscar o conteúdo simbólico.  Este trabalho explora dois exemplos clássicos de ilustrações simbólicas que aparecem no Livro Dois, Capítulo xxvii dos Três livros de Filosofia Oculta [i], [ii] pelo notável Alquimista do século XVI, Henry Cornelius Agrippa, intitulados “Da Proporção, Media e Harmonia do Corpo Humano”. Estes símbolos são figuras geométricas muito complexas, acompanhadas por referências obscuras a conceitos filosóficos.  A exploração intentada neste trabalho enfocará especificamente as propriedades geométricas das figuras.

Figuras de Agrippa

As relações proporcionais exclusivas mostradas pelo corpo humano parecem ter sido conhecidas em tempos antigos. Vitrúvio (cerca de 30 A.C) no Livro III de seu tratado De Architecture [iii] detalhou estas proporções por escrito como segue:

“O umbigo está naturalmente posicionado no centro do corpo humano e, se em um homem deitado com sua face para cima, e suas mãos e pés estendidos, de seu umbigo como centro, um círculo pode ser descrito, ele tocará seus dedos das mãos e dos pés. Não é somente por um círculo que o corpo humano é assim circunscrito, como pode ser visto, colocando-o dentro de um quadrado. Porque se medindo dos pés até o topo da cabeça, e, então os braços totalmente estendidos, descobrimos que esta última medida é igual à primeira; de modo que linhas nos ângulos retos entre si, fechando afigura, formarão um quadrado.”

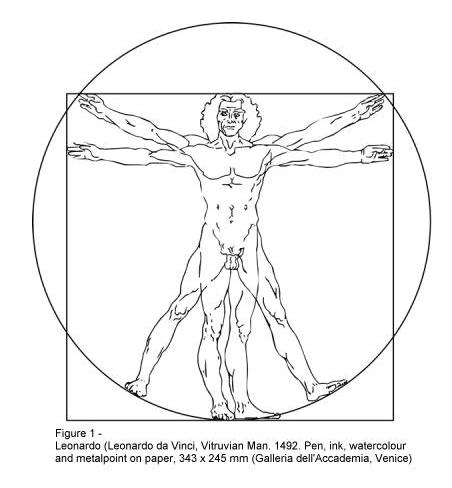
Esta descrição (cerca de 1487) foi usada por Leonardo Da Vinci para criar o famoso desenho intitulado o Homem Vitruviano.

(Figura 1) [iv] Figuras semelhantes à de Leonardo foram criadas durante um longo período (algumas antes, algumas depois) por Filósofos e Artistas, tais como Hildegard von Bingen (1098-1179), Fra Giovanni Giocondo (1435-1515), Bartolommeo Caporali  (1442-1509),  Cessare  Cesariano  (1483-1543),  Francesco  di  Georgio  (1482-1489),  Robert  Fludd  (1617) e Eliphas Levi (1810-1875).

 

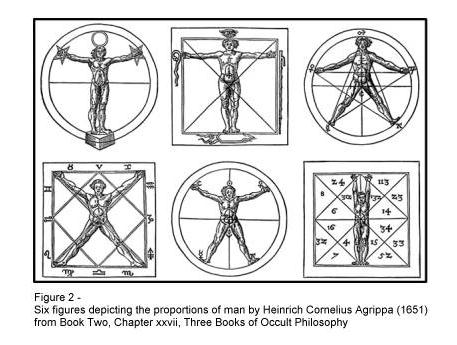
Agrippa, provavelmente, tinha conhecimento de muitos destes desenhos quando em 1651 ele publicou seus Três Livros de filosofia Oculta. As seis figuras publicadas por Agrippa no Livro Dois, Capítulo xxvii são, à primeira vista, bastante semelhantes ao Homem Vitruviano (a figura 2 é uma colagem destas figuras [v]). Nestas figuras, Agrippa simbolicamente sugere, fechando o home em um círculo (ele mesmo um símbolo de perfeição e infinito) sua relação (do homem) com o reino cósmico ou divino. Outra destas figuras ilustra a forma humana com os braços estendidos (semelhante ao Homem Vitruviano) encerrada em um quadrado, ilustrando a “medida de quatro quadrados” onde o home “fará uma quadratura equilateral” [vi].

 

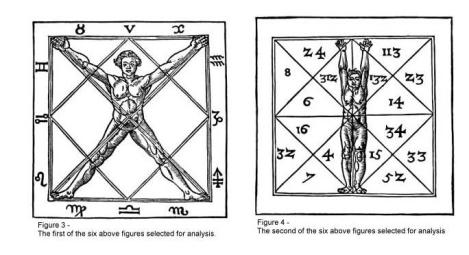
Selecionei duas destas seis figuras para análise, e elas são reproduzidas abaixo como Figura 3 e Figura 4.   Favor notar que embora o restante das figuras de Agrippa no Capítulo xxvii também seja imensamente interessantes, estas duas compartilham um tema simbólico comum e têm propriedades geométricas idênticas. Limitação de espaço não permite que outras figuras sejam totalmente discutidas ou ainda mais desenvolvidas, embora elas sejam rapidamente consideradas em relação às duas figuras de interesse.

 

 

Propriedades geométricas

Os conceitos geométricos representados por ambas Figura 3 e Figura 4 são essencialmente idênticos. Na realidade, a análise destas figuras é mais bem abordada tratando-as como uma única figura composta, combinando certos elementos de cada uma delas.  Duas características exclusivas das figuras são especialmente notáveis. Primeiro, a posição do corpo da forma humana na Figura 3 é tal que os braços e pernas estão alinhados com a diagonal do Quadrado em que ela aparece. A posição do corpo da forma na Figura 4, por outro lado, está alinhada com a dimensão da altura do quadrado. É um ponto importante reconhecer que se a forma humana na Figura 3 for girada em torno de seu ponto central (o umbigo), as mãos e pés traçarão um círculo que circunscreve exatamente o quadrado. Também, com relação aos símbolos do zodíaco que aparecem na Figura 3, o leitor notará que o zodíaco é exibido tipicamente em formato circular, correspondendo à esfera celestial. O fato de que os símbolos do zodíaco aparecem na borda, como eles o fazem nesta figura, pede ao observador que visualize um círculo inscrito dentro do quadrado externo. Favor notar também que os símbolos do zodíaco também são críticos para um entendimento da interpretação filosófica da figura.

Na Figura 4, as mãos e pés da forma humana, quando giradas de maneira semelhante, traçarão um círculo que é exatamente inscrito no quadrado.  A Figura 4 exige que para análise geométrica, ignoremos temporariamente os valores numéricos que aparecem em cada uma das seções triangulares do desenho.  Observe que ausente a forma humana, a Figura 4 se parece com a Figura 3, exceto que duas linhas adicionais foram adicionadas perpendicularmente uma à outra e interceptando-se no centro.

A Figura 5 é uma composição da Figura 3 e da Figura 4, ausente a forma humana, zodíaco e números e com as formas geométricas rotuladas para facilitar a discussão. A Figura 5 adiciona, entretanto, dois círculos concêntricos à composição. Um dos dois quadrados (ABDC), portanto, parece circunscrito em relação ao círculo maior, e o outro (EFGH) parece inscrito no círculo menor. Estes quadrados estão dispostos de tal forma que as diagonais do quadrado EFGH (Linha FH e Linha EG) são tanto os diâmetros do círculo, quanto a altura e largura, respectivamente do quadrado ABDC.   As múltiplas interseções das diagonais dos quadrados e das diagonais com os lados dos quadrados produzem não menos que dezesseis (16) triângulos isósceles idênticos.

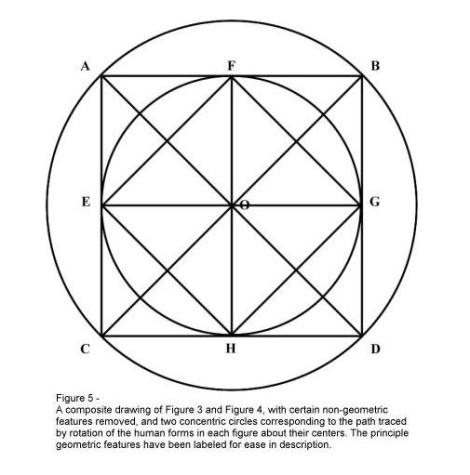
Não é especialmente difícil determinar a significância geométrica subjacente destas figuras.  O leitor poderá prontamente distinguir que a área do Quadrado ABDC é duas vezes aquela do quadrado EFGH, baseado estritamente no fato de que o raio dos dois círculos está em uma relação de 2:1 com relação ao outro. Isto, naturalmente, coloca a altura dos dois quadrados em uma relação semelhante, e também a área dos quadrados.

A conseqüência desta figura é, então, que quando um quadrado está circunscrito em relação a um círculo, sua área será duas vezes aquela de um quadrado inscrito no mesmo círculo. O dois círculos concêntricos na Figura 6 compartilham um relacionamento semelhante; a saber a área do círculo circunscrito em relação ao Quadrado ABDC tem duas vezes a área do círculo inscrito no Quadrado ABDC. Este conceito é resumido no Livro de Arquimedes de Lemmas [vii], Proposta 7 onde é afirmado:

“Se círculos são circunscritos em relação ao outro e inscritos em um quadrado, o círculo circunscrito é o dobro do quadrado inscrito.”

A Proposta 7 é conhecida como a base pela qual Arquimedes aproximou o valor de Pi (3,14159…) usando seu famoso método de exaustão [viii]. Este conceito está também refletido por Euclides no Livro XII de Elementos, Proposição 1 [ix].   Estas figuras foram cruciais na descoberta, mais tarde, das (Figura 6) propriedades matemáticas da luna de Hipócrates [x] (Uma luna é uma figura plana limitada por dois arcos circulares de raios diferentes, i.e. um crescente [xi]) por Euler em 1771 [xii]. As figuras de Agrippa ilustradas aqui e também a luna ocuparam uma posição proeminente na procura imemorial da “Quadratura do Círculo”. Isto foi, naturalmente, antes da descoberta de que o valor de Pi era um número indeterminado.

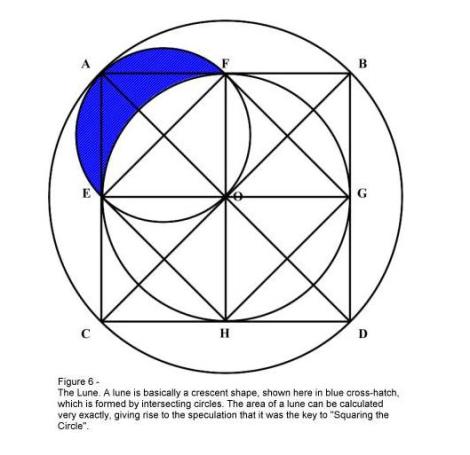
Observe-se que na Figura 6, o Quadrado ABDC é quatro vezes maior do que o Quadrado AFOE. A diferença em áreas relativas dos dois quadrados e também dos dois círculos formando a Luna são, portanto, proporcionais.

Em seu livro, A Música de Pitágoras [xiii], a autora Kitty Ferguson descreve uma cena de Meno de Platão onde Sócrates e Meno estão discutindo a figura de um quadrado de quatro pés que Sócrates desenho na areia. É relatado que durante a discussão, Sócrates usa este quadrado como base para a construção de uma figura idêntica àquela mostrada na Figura 5, menos os círculos. Enquanto desenvolvia esta figura, Sócrates conduz um dos servos de Meno em um diálogo onde o servo deduz que a área do quadrado maior é duas vezes aquela do quadrado menor. Toda a finalidade desta cena em Meno é ilustrar que o homem é capaz de desenvolver conhecimento por dedução, e não depender simplesmente de conhecimento prévio, ou conhecimento que já está totalmente desenvolvido e presente no nascimento. Não há dúvida, as figuras publicadas mais tarde por Agrippa incluem o simbolismo da capacidade do homem de discernir e empregar raciocínio dedutivo.  Entretanto, são os princípios Geométricos e não os Filosóficos que são de interesse neste trabalho; é notável com relação a isso que duas figuras de interesse ilustram características proporcionais da forma humana que não estão diretamente relacionadas com a Média Dourada (Phi ou a Proporção divina). Este não é o caso com o Homem Vitruviano de Leonardo, nem é o caso com as figuras restantes oferecidas por Agrippa (como mostra a Figura 2).

Isto não quer dizer que o valor de Phi não pode ser desenvolvido usando estas duas figuras, que ele pode claramente ser (Figura 7).  Entretanto, o valor de Phi não coincide com características distintas do corpo nestas figuras. O fato de que estas figuras sejam incluídas com uma série de esquemas que claramente descrevem as proporções Phi do corpo humano nos levariam a acreditar que Agrippa considerava as relações geométricas entre quadrados e círculos inscritos e circunscritos como suficientemente não-coincidentes, a ponto de serem consideradas evidências da origem divina do Homem.

Isto é de interesse especial para a Maçonaria, uma vez que duas figuras sendo discutidas revelam proporções geométricas absolutas na forma humana, e não dependem de princípios matemáticos (isto é, não-geométricos) para apresentar este argumento.

 

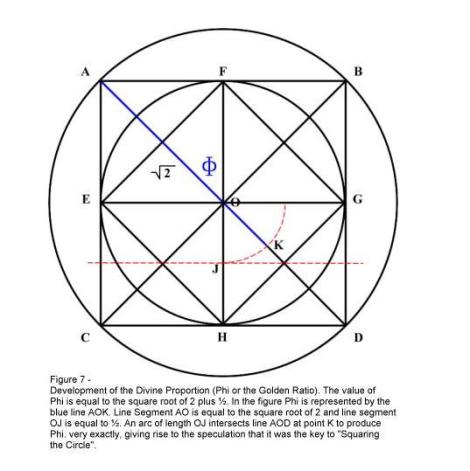
Na Figura 7, consideremos o quadrado AFEO. Se presumirmos que os lados deste quadrado têm um valor dimensional de uma (1) unidade, então a diagonal deste quadrado (linha AO) tem um valor igual à raiz quadrada de dois. O valor de Phi é associado muito de perto com a raiz quadrada de dois, sendo igual à raiz quadrada de dois mais meio (1,414213 + 0,5 = 1,614213).  Portanto, para demonstrar o valor de Phi em nossa figura, temos apenas que adicionar o valor de meia unidade à diagonal AO. Conseguimos isso, bisseccionando a linha OH, construindo uma linha através dos centros dos quadrados ECHO e GDHO, criando o Ponto J e, portanto, segmento de linha OJ. Desenhando um arco de comprimento OJ usando o Ponto O como centro, de tal forma que ele interrompa a linha OD (no ponto K), formamos o segmento de linha OK. Toda a linha AK, então, tem um comprimento igual à raiz quadrada de dois mais meio, que é o valor de Phi.

Heráclito (540-480) recebeu o crédito por dizer “O homem é a medida de todas as coisas” [xiv]. Esta Figura é, assim como são as duas figuras na Filosofia Oculta de Agrippa, a representação geométrica do Homem como criação divina, centrado no universo, com as faculdades dadas por Deus da razão, e fisicamente formadas em proporção divina.

NOTAS:

[i] Agrippa, Heinrich Cornelius. (1995). Three Books of Occult Philosophy. In Donald Tyson (Ed.). The Foundation Book of Western Occultism.  Llewellyn. ASIN: B000KT6YLK.

[ii] Agrippa of Nettesheim, Heinrich Cornelius. (1651). Three Books of Occult Philosophy. Book 2. London. In Joseph H. Peterson (Ed.). [Digital  Edition] . Retrieved June 18, 2008, from http://www.esotericarchives.com/agrippa/agrippa2.htm.

[iii] Vitruvius, Pollio. De Architectura (The Ten Books on Architecture). In Project Gutenberg (2006). Retrieved June 18, 2008, from  http://www.gutenberg.org/etext/20239.

[iv] Image Source: The Ohio State University Fine Arts Library. Retrieved June 18, 2008, from http://library.osu.edu/blogs/finearts/2008/02/14/be- mine-frank-ohara/.

[v] Hatzigeorgiou, Karen J. (2008). Public Domain Images Reproduced by Agreement of Terms of Publication. Retrieved June 18, 2008, from  http://karenswhimsy.com/sacred-geometry.shtm.

[vi] Agrippa von Nettesheim, Cornelius. (1651) De Occulta Philosophia Libri Tres. Edited by V. Perrone Compagne. in Studies in the History of  Christian Thought, 48. Leiden: Brill. (1992).

[vii] Archimedes. in Bogomolny, Alexander, Archimedes’ Book of Lemmas from Interactive Mathematics Miscellany and Puzzles. Retrieved June 23,  2008 from  http://www.cut-the-knot.org/Curriculum/Geometry/BookOfLemmas/index.shtml.

[viii] Carothers Neal. Archimedes’ Method of Exhaustion. Department of Methematics and Statistics. Bowling Green State University. Retrieved June  22, 2008 from http://personal.bgsu.edu/~carother/pi/Pi3a.html.

[ix] Euclid’s Elements, Book XII. In Joyce, D.E. (1997) Euclid’s Elements. Clark University. Retrieved June 22, 2008 from http://aleph0.clarku.edu/~djoyce/java/elements/bookXII/propXII2.html.

[x] Sandifer, Charles Edward. (2007). The Early Mathematics of Leonhard Euler. The Mathematical Association of America – Tercentenary Euler http://www.freemasons-freemasonry.com/occult_philosophy.html 27/7/2008 Celebration. Vol. 1.Washington, D.C. ISBN:0883855593

[xi] Weinstein, Eric. (2008). Lune. Wolframs Math World. Wolfram Research. Retrieved June 22, 2008. From http://mathworld.wolfram.com/Lune.html

[xii] Euler, M.J.A. Réflexions Sur la Variation de la Lune. Publication l’Académie 1766, 18 pp.

[xiii] Ferguson, Kitty. The Music of Pythagoras. (2008). New York. Walker & Company. Macmillan (Dist.)  ISBN-10: 0-8027-163-8; ISBN-13: 978-0-   8027-1631-6. pp. 140-145.

[xiv] Hemenway, Priya & Ray, Amy. (2005). Divine Proportion: Phi in Art, Nature, and Science. Sterling. ISBN:1402735227. pp. 92.